
Nikolaus PetryFuzzy-LogikJurPC Web-Dok. 131/1998, Abs. 1 - 49 |
Gliederung: |
1. Einleitung |
| Fuzzy-Logik ist die Bezeichnung für alle Methoden, die sich mit der Modellierung von Daten und Regeln befassen, die in unscharfer Form vorliegen. Seit fast 10 Jahren taucht dieser Begriff selbst in Tageszeitungen und in Werbekampagnen auf. | JurPC Web-Dok. 131/1998, Abs. 1 |
| 1965 veröffentlichte Lotfi Zadeh, Professor an der University of California in Berkeley, seinen Aufsatz "Fuzzy Sets" (Unscharfe Mengen). In der Folge wurde eine Vielzahl theoretischer Arbeiten zu diesem Thema veröffentlicht. Praktische Anwendungen wurden zuerst in Europa (1974: Regelung eines Dampferzeugers in einem Kraftwerk, 1976: Steuerung eines Zementbrennofens 1978 in Dänemark,) umgesetzt, Fuzzy-Logik hatte aber keinen Durchbruch in Europa. | Abs. 2 |
| In Japan wurde etwas später mit der Umsetzung begonnen (z.B. die Steuerung der Untergrundbahn in Sendai 1987). Mit der Gründung verschiedener Institute (unter anderem IFSA: International Fuzzy Systems Association, LIFE: Laboratory for international Fuzzy Engineering Research), die zum Teil vom japanischen Industrie- und Handelsministerium MITI finanziert wurden, begann die Massenproduktion von Produkten, die in Teilen oder vollständig durch Fuzzy-Technologie gesteuert werden. | Abs. 3 |
| Überall dort, wo menschliches Expertenwissen vorhanden ist, dieses Wissen aber nur mit komplizierten Modellen oder aber überhaupt nicht, weil nicht widerspruchsfrei, mathematisch modellierbar ist, kann die Fuzzy Logik weiterhelfen. | Abs. 4 |
| Das Abbremsen eines vollbesetzten U-Bahn-Zuges kann ein guter Lokführer so durchführen, daß der Zug ruckfrei in optimaler Zeit am richtigen Platz stehenbleibt. Der Vorgang ist nur schwer mathematisch modellierbar und kompliziert in der technischen Umsetzung. Das Wissen um die optimale Bremskraft hat sich der Lokführer in unzähligen Bremsvorgängen angeeignet, er kann es aber nur in Form unscharfer Regeln wie z.B. "Ist der Zug vollbesetzt, muß ich stärker bremsen, als wenn der Zug leer ist" angeben. Im japanischen Sendai wurde eine Fuzzy-Steuerung für eine U-Bahn entwickelt, die die Züge nicht nur schneller und exakter, sondern auch mit einem gegenüber vorher um 10 % geringeren Verbrauch fahren läßt. | Abs. 5 |
| Die Brockhaus-Enzyklopädie beschreibt Fuzzy-Logik als ein "... Logik-System, das im Gegensatz zur gewöhnlichen Logik nicht nur zwei Wahrheitswerte kennt, sondern mehrere bis unendlich viele (...). Die Fuzzy-Logik ermöglicht dann mit relativ geringem Aufwand die Verarbeitung von menschlichem Wissen und Erfahrungen, die nur in sprachlicher ("linguistischer") Form vorliegen, mit dem Computer." | Abs. 6 |
| Anwendungsgebiete von Fuzzy-Logik sind also überall dort, wo Wissen in Form unscharfer Regeln vorliegt. Kosko faßt es kurz zusammen in "Fuzzy-Logik ist das Argumentieren mit unscharfen Mengen". Um Fuzzy-Logik anwenden zu können, muß man Fuzzy-Mengen verstehen, da die Elemente der Fuzzy-Logik gerade diese unscharfen Mengen sind. Dazu gehört ein bestimmtes mathematisches Instrumentarium, das nur wenig mehr als die klassische Mengenlehre umfaßt. | Abs. 7 |
2. Mengenlehre |
2.1 Klassische Mengen |
| Die klassische Mengentheorie basiert auf der Annahme, daß für jedes Element einer Grundgesamtheit Wgesagt werden kann, ob es in einer Menge A liegt oder nicht. Alle Menschen können idealisierend einer der beiden Kategorien Mann bzw. Frau zugeordnet werden. Aus der Menge aller Bürger mit Geburtsurkunde ist die Menge derer, die vor 1964 geboren sind, exakt angebbar. Mathematisch ist die Aufzählung der Elemente einer Menge A äquivalent zur Angabe der sog. Indikatorfunktion mA. Die Funktion mA nimmt nur die Werte 1 oder 0 an. Sie nimmt für ein Element w den Wert 1 an, wenn w in der Menge A liegt, und sie nimmt den Wert 0 an, wenn w nicht in der Menge A liegt. Zur Vereinfachung der grafischen Darstellung wird im Folgenden als Grundgesamtheit W die Menge R+ der nichtnegativen reellen Zahlen genommen. | Abs. 8 |
| Zur Verdeutlichung des klassischen Konzeptes einer Menge wird eine exemplarische Stelle in Gesetzestexten betrachtet, an denen Zahlenwerte als explizite Grenzen erwähnt werden. In den Begriffsbestimmungen § 7 SGB VIII werden definiert: | Abs. 9 |
| 1. Im Sinne dieses Buches ist (...) 3. junger Volljähriger, wer 18, aber noch nicht 27 Jahre alt ist, 4. junger Mensch, wer noch nicht 27 Jahre alt ist. | Abs. 10 |
| Die Altersstufen, die junge Volljährige definieren, werden zu einem Intervall zusammengefaßt, wobei die eine Grenze (18 Jahre) enthalten, die andere Grenze (27 Jahre) ausgeschlossen ist. Bezeichnet man mit A die Menge der Lebensalter junger Volljähriger und mit mA die Indikatorfunktion dieser Menge, so kann grafisch die Indikatorfunktion und somit die Menge A wie folgt dargestellt werden: | Abs. 11 |
| Die Grafik besagt, daß z.B. das Alter 16 und das Alter 29 einen Indikatorwert 0 erhalten, mit der Bedeutung, daß 16 bzw. 29 nicht zur Menge A der Lebensalter junger Volljähriger gehören. Hingegen gehören das Alter 20 und 25 zur Menge A. Die gefüllten Punkte markieren die Funktionswerte an der jeweiligen Sprungstelle, d.h. das Alter 18 gehört mit dem Wert 1 (also ganz) zu den Lebensaltern junger Volljähriger, und das Alter 27 gehört mit dem Wert 0 (also gar nicht) zu den Lebensaltern junger Volljähriger. | Abs. 12 |
| Entsprechend sieht die grafische Darstellung der Lebensalter junger Menschen aus, die zugehörige Menge sei mit B und die zugehörige Indikatorfunktion mit mB bezeichnet: | Abs. 13 |
| § 7 Abs 1 Satz 4 SGB VIII gibt eine scharfe Grenze vor bei der Einordnung eines Menschen in die Alterstufe junger Menschen. Diese Eigenschaft der scharfen Grenzziehung ist charakteristisch für die klassische Mengenlehre: ein Element gehört entweder ganz oder gar nicht zu einer Menge. | Abs. 14 |
2.2. Fuzzy-Mengen |
| Dem Gesetzgeber ist bewußt, daß eine solche scharfe Grenzziehung nicht adäquat zur Duchsetzung der Ziele beim Angebot von Jugendarbeit ist. Daß die Zuordnung eines Menschen in die Gruppe der jungen Menschen nicht nur vom Alter abhängen darf, wird zum Beispiel deutlich in § 11 SGB VIII (Jugendarbeit): | Abs. 15 |
| (1) Jungen Menschen sind die zur Förderung ihrer
Entwicklung erforderlichen Angebote der Jugendarbeit zur Verfügung zu
stellen. (...) (4) Angebote der Jugendarbeit können auch Personen, die das 27. Lebensjahr vollendet haben, in angemessenem Umfang einbeziehen. | Abs. 16 |
| § 11 Abs 4 SGB VIII gibt nun auch nicht eindeutig wieder, bis zu welchem Alter auch nicht junge Menschen in die Angebote der Jugendarbeit einbezogen werden können. Folgende Interpretation aus der Sicht der Fuzzy-Theorie ist aber möglich: | Abs. 17 |
| 1. Alle Menschen, die noch nicht 27 Jahre alt sind, gehören vollständig zu den durch Jugendarbeit förderungsfähigen Menschen. | Abs. 18 |
| 2. Menschen, die 27 Jahre oder älter sind, gehören zu einem gewissen, "angemessenen" Grad zu den durch Jugendarbeit förderungsfähigen Menschen. | Abs. 19 |
| 3. Es gibt ein Alter, ab dem Menschen nicht mehr zu den durch Jugendarbeit förderungsfähigen Menschen gehören. | Abs. 20 |
| In der Fuzzy-Theorie wird dieser "angemessene Umfang" durch Zugehörigkeitswerte modelliert. Ein Zugehörigkeitswert ist entweder 0 oder 1 oder eine Zahl zwischen 0 und 1. Die Semantik ergibt sich aus der Erweiterung der klassischen Mengenlehre: bezeichnet man die unscharfeMenge der durch § 11 Abs 1 und Abs 4 SGB VIII bezeichneten Menschen mit C, so bedeutet ein Zugehörigkeitswert 1 eines Alters x zur Menge C, daß dieses Alter x vollständig zur Menge C gehört. Ein Zugehörigkeitswert 0 eines Alters y zur Menge C bedeutet, daß dieses Alter y gar nicht zur Menge C gehört. Ein Zugehörigkeitswert zwischen 0 und 1 (z.B. 0,75) eines Alters z zur Menge C bedeutet, daß dieses Alter z zu diesem Grade (z.B. 0,75) zur Menge C gehört. | Abs. 21 |
| Die Definition einer Fuzzy-Menge kann auf verschiedene, äquivalente Arten erfolgen. Die für die Modellierung von linguistischer Unschärfe praktikabelste Definition ist folgende: eine Fuzzy-Menge C ist eine Abbildung mC: R+ ®[0,1] von den nichtnegativen reellen Zahlen R+ in das Intervall [0,1]. Die Abbildung mC wird sowohl Fuzzy-Menge als auch Zugehörigkeitsfunktion der Fuzzy-Menge C genannt. | Abs. 22 |
| In der Fuzzy-Theorie wird immer versucht, die funktionalen Zusammenhänge möglichst einfach zu gestalten. Dabei werden Grenzpunkte oft durch Geradenstücke verbunden, um so für die zwischen den Grenzpunkten liegenden Werte Zugehörigkeiten berechnen zu können. Zur Verdeutlichung werde hier angenommen, daß der Umfang, zu dem Menschen über 27 Jahre durch Jugendarbeit gefördert werden können, nur vom Alter abhänge, und daß Menschen über 35 Jahre gar nicht durch Jugendarbeit gefördert werden können. Daraus ergibt sich folgende grafische Darstellung, wobei auf der Abszisse das Lebensalter und auf der Ordinate der Umfang der Förderung, normiert auf den Wert 1 für vollständige Förderung und den Wert 0 für keine Förderung abgetragen sind: | Abs. 23 |
|
| Vergrößert man die Grafik im Bereich 25 bis 40, so kann man sehr einfach die Zugehörigkeitswerte dieser Alterstufen ablesen. Das Alter 29 hat gerade eine Zugehörigkeit von 0,75 zur Menge C der förderungsfähigen Menschen. | Abs. 24 |
| Mit Fuzzy-Mengen ist es möglich, unscharfe Informationen mathematisch zu modellieren. Insbesondere unscharf vorliegende numerische Informationen können mit Fuzzy-Mengen klarer dargestellt werden. Es ist oft einfach nicht möglich, eine scharfe Grenze anzugeben, bis zu der oder ab der eine Eigenschaft zu gelten hat. Die Übergänge sind meist fließend von "gar nicht vorhanden" zu "vollständig vorhanden" oder umgekehrt. Es ist eben nicht so, daß ein Mensch von 27 Jahren und 1 Tag plötzlich kein junger Mensch mehr ist. Gibt man sich die Grenze vor, ab der die Eigenschaft "junger Mensch" sicher nicht mehr gilt (im obigen Beispiel 35 Jahre), so kann für jedes Alter zwischen 27 Jahren und 35 Jahren ein Grad der Zugehörigkeit dieses Alters zu der Menge der jungen Menschen einfach angegeben werden. | Abs. 25 |
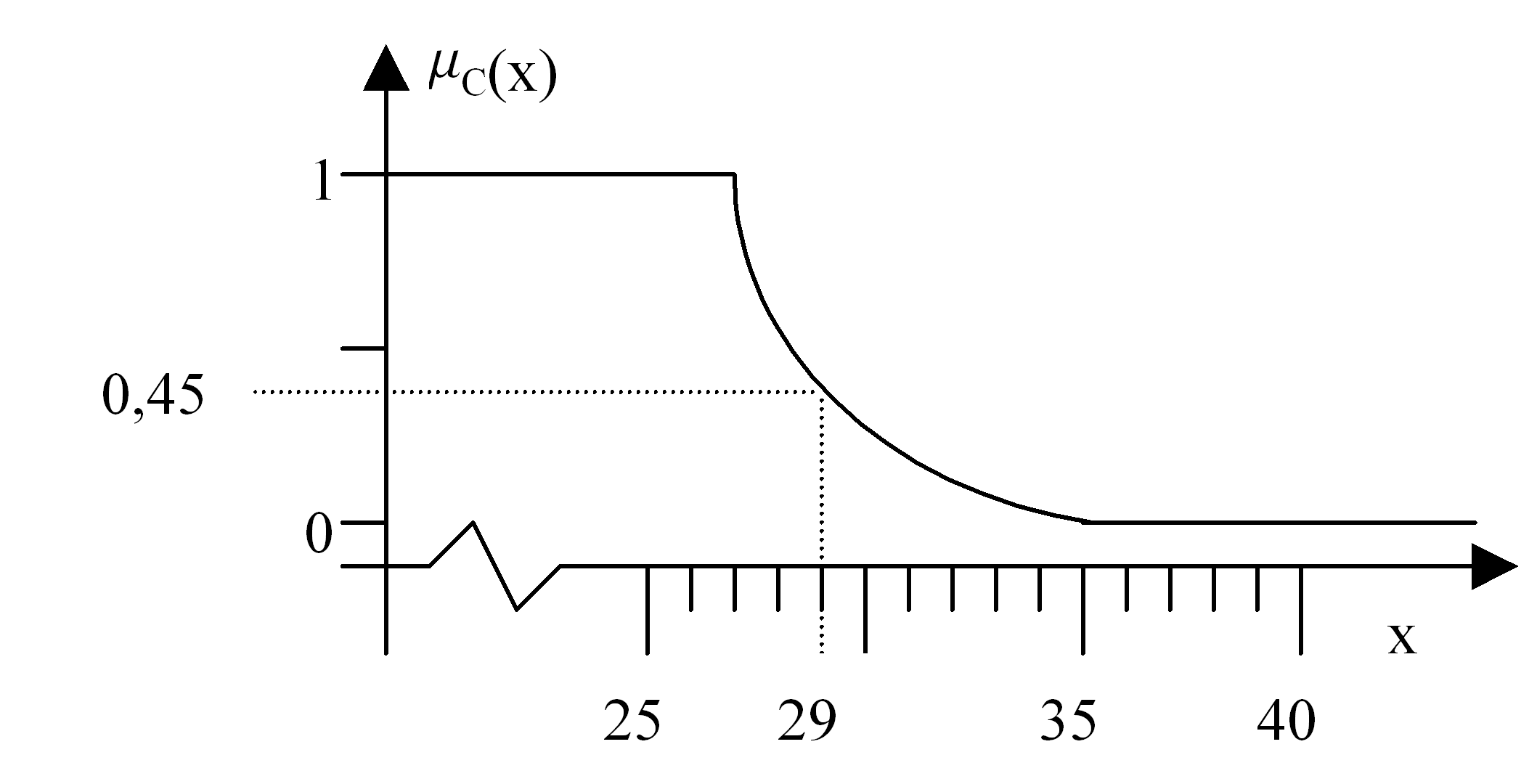 |
| Die Fuzzy-Theorie erlaubt neben der Modellierung mit Geradenstücken auch weitere, kompliziertere Funktionstypen zur Berechnung der Zugehörigkeitswerte. Verwendet man in obigem Beispiel etwa ein nach oben geöffnetes Parabelstück, um die beiden Grenzpunkte zu verbinden, so ergibt sich für das Alter 29 ein Zugehörigkeitswert von 0,45 (wobei der exakte Wert von weiteren Parametern der Parabel abhängt). | Abs. 26 |
| Bei der Modellierung der linguistischen Unschärfe ist der exakte Verlauf der Zugehörigkeitsfunktion zwischen solchen Grenzpunkten meist nicht wesentlich. Wichtig ist die Festlegung der Grenzpunkte, d.h. es muß klar sein, welche Elemente vollständig zur Menge gehören sollen (also Zugehörigkeit 1 erhalten sollen) und welche Elemente sicher nicht zur Menge gehören sollen (also Zugehörigkeit 0 erhalten sollen). Erst wenn man die Zugehörigkeit beim Überschreiten einer Grenze z.B. nur langsam sinken lassen möchte, bietet es sich an, andere als lineare Funktionstypen zu verwenden. | Abs. 27 |
|
| Auch Sprünge in der Zugehörigkeit können modelliert werden. Hält man z.B. eine nur zehnprozentige Förderung für unpraktikabel, so kann man den Förderungsanteil von 100 % bei 27 Jahren auf 25 % bei den unter 35-Jährigen abfallen und danach auf Null fallen lassen. | Abs. 28 |
| In praktisch allen Lebensbereichen werden unscharfe Begriffe verwendet: "ein großer Mensch", "eine hohe Geschwindigkeit", "grob fahrlässig", "schwere Körperverletzung" sind nur eine kleine Auswahl. | Abs. 29 |
| Die Theorie der Fuzzy-Mengen erlaubt die mathematische Modellierung von unscharfen Begriffen. Das alleine hilft manchmal schon weiter, besonders dann, wenn man quantifizieren möchte, was man sonst nur sprachlich formulieren kann. Z.B. "hohe Inflationsrate" erlaubt viele Interpretationen. Die Angabe einer Fuzzy-Menge, die zu jeder Inflationsrate eine Zugehörigkeit angibt, zu der man diese Inflationsrate als "hoch" ansieht, macht den Begriff verständlicher und erlaubt es, Kritik an passender Stelle anzubringen. | Abs. 30 |
| Fuzzy-Mengen sind weiterhin zu betrachten als Hilfsmittel für die Fuzzy-Logik. Mit Hilfe der Fuzzy-Logik können Regeln mit unscharfen Prämissen und unscharfen Konklusionen mathematisch modelliert werden. | Abs. 31 |
3. Verknüpfungen von Fuzzy-Mengen |
3.1 Die "UND"-Verknüfung |
| Mengen werden häufig durch Angaben der Eigenschaften der Elemente angegeben. Das Intervall [18,27] ist gleich der Menge aller reellen Zahlen x, die gleichzeitig zwei Eigenschaften erfüllen: x³ 18 und x<27. Eine Zahl xgehört genau dann zum Intervall [18,29], wenn sie beide Eigenschaften gleichzeitig erfüllt. | Abs. 32 |
| Die Übertragung von mengentheoretischen Verknüpfungen auf Fuzzy-Mengen wurde mit dem Ziel entwickelt, daß bei Anwendung der Grundoperationen auf scharfe Mengen die bekannten Ergebnisse geliefert werden. Das führt zu vielen Möglichkeiten, von denen sich eine, der sogenannte min-Operator, in weiten Teilen der Fuzzy-Control durchgesetzt hat: Sind A und B zwei Fuzzy-Mengen über derselben Grundmenge mit Zugehörigkeitsfunktionen mA und mB, so gilt für die Zugehörigkeitsfunktion der Fuzzy-Menge AÙB: | Abs. 33 |
| mAÙ B(x) = min{ mA (x), mB(x)} | Abs. 34 |
| Die Zugehörigkeit eines Elementes zu beiden Fuzzy-Mengen A und B ist gleich dem Minimum der beiden einzelnen Zugehörigkeiten. Bildlich gesprochen bildet das schwächste Glied der Kette die gemeinsame Stärke. Als Beispiel betrachte man die Fuzzy-Menge A der Zahlen "etwa 18 und größer" und die Fuzzy-Menge B der Zahlen "etwa 27 und kleiner". Die beiden Fuzzy-Mengen können durch folgende Zugehörigkeitsfunktionen beschrieben werden, wobei in dieser Modellierung angenommen wird, daß Zahlen zwischen 15 und 18 zu einen positiven Grad als zu der Menge zugehörig angesehen werden: | Abs. 35 |
|
| Für "A und B" erhält man aufgrund des Minimumoperators folgende Fuzzy-Menge: | Abs. 36 |
|
| Sind die Fuzzy-Mengen A und B über verschiedenen Grundbereichen, so kann man die Fuzzy-Menge der Paare bestimmen, die zu beiden Fuzzy-Mengen gleichzeitig gehören: | Abs. 37 |
| mAÙB((x,y)) = min{mA(x), mB(y)} | Abs. 38 |
| Die ist insbesondere in der Fuzzy-Logik wichtig, wo die Prämissen des Modus Ponens häufig aus zwei mit "und" verknüpften Aussagen bestehen. | Abs. 39 |
3.2. Die "ODER"-Verknüfung |
| Hat man zwei Mengen A und B über derselben Grundgesamtheit und bildet deren Vereinigung, so erhält man alle Elemente, die mindestens eine der Eigenschaften erfüllen, die die beiden Mengen beschreiben. Dabei kann es auch Elemente geben, die beide Eigenschaften erfüllen. Man spricht vom "nicht-exklusiven ODER", im Gegensatz dazu verknüpft der "XOR"-Operator Mengen dadurch, daß nur die Elemente beschrieben werden, die genau eine der beschreibenden Eigenschaften erfüllen. | Abs. 40 |
| Die Übertragung auf Fuzzy-Mengen erfolgt ebenfalls wieder unter Berücksichtigung der Kompatibilität mit dem ODER-Operator der scharfen Mengen. Dabei haben sich im Laufe der Zeit zwei Operatoren durchgesetzt: der MAX-Operator und die "algebraische Summe". | Abs. 41 |
| Sind A und B zwei Fuzzy-Mengen über derselben Grundmenge mit Zugehörigkeitsfunktionen mA und mB, so gilt für die Zugehörigkeitsfunktion der Fuzzy-Menge AÚB: | Abs. 42 |
| mAÚB(z) = max{mA(z), mB(z)} | Abs. 43 |
| Erfüllt ein Element mindestens eine von zwei Eigenschaften A und B mit einem positiven Zugehörigkeitsgrad, so hat diese Element auch eine positive Zugehörigkeit zur Fuzzy-Menge AÚB. Die Anwendung der Maximum-Regel erfolgt unter der Annahme, daß ein Element x (bzw. ein Paar (x,y)) zur Fuzzy-Menge AÚB keine größere Zugehörigkeit haben kann als zu jeder der beiden Einzelmengen. Hat ein Element den Zugehörigkeitswert Null zu beiden Fuzzy-Mengen A und B, so hat es auch den Zugehörigkeitswert Null zur Fuzzy-Menge AÚB. | Abs. 44 |
| Als Beispiel werden die beiden Fuzzy-Intervalle "etwa [14,18]" und "etwa [20,24]" vereinigt: | Abs. 45 |
|
| Die Anwendung der Maximum-Regel ergibt eine Fuzzy-Menge, deren Zugehörigkeitswerte sich aus den Maxima der einzelnen Zugehörigkeiten errechnen. | Abs. 46 |
|
| Der zweite Operator zur Bildung von AÚB ist die algebraische Summe. Sind A und B zwei Fuzzy-Mengen über derselben Grundmenge mit Zugehörigkeitsfunktionen mAund mB , so gilt für die Zugehörigkeitsfunktion der Fuzzy-Menge AÚB: | Abs. 47 |
| mAÚB(z) = mA(z) + mB(z) - mA(z) · mB(z) ( = mA(z) + mB(z) (1 - mA(z))) | Abs. 48 |
| Mit der Formel in den Klammern sieht man, daß sich mit
dieser Form der Modellierung immer Zugehörigkeiten größer als
das Maximum der einzelnen Zugehörigkeiten ergeben, die aber dennoch immer
kleiner oder gleich Eins sind. Mit der algebraischen Summe werden gleiche Zugehörigkeiten
verstärkt (z.B. ergeben Zugehörigkeiten mA(z)
= 1/2 und mB(z)=1/2 einen Wert
mAÚB(z)=3/4=0,75).
Dagegen führen stark unterschiedliche Zugehörigkeiten nicht zu einem
entsprechenden Anstieg (z.B. ergeben Zugehörigkeiten mA(z)
= 1/2 und mB(z)=1/8 einen Wert
mAÚB(z)=9/16=0,5625).
| JurPC Web-Dok. 131/1998, Abs. 49 |
| Anm. der Redaktion: Der Beitrag wird in Kürze fortgesetzt. |
| [online seit: 04.09.98] |
| Zitiervorschlag: Autor, Titel, JurPC Web-Dok., Abs. |
| Zitiervorschlag: Petry, Nikolaus, Fuzzy-Logik - JurPC-Web-Dok. 0131/1998 |